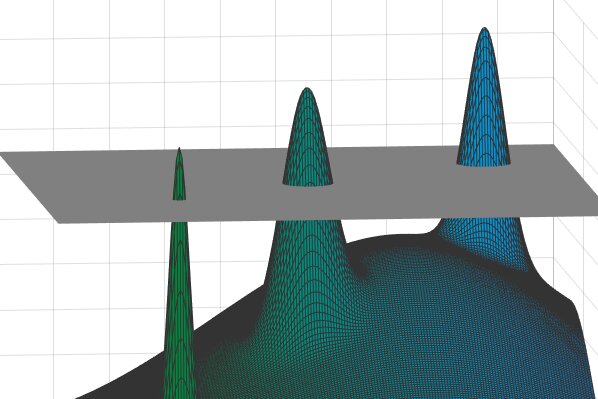
Dalam beberapa kasus, diameter setiap puncak akan jauh lebih kecil daripada jarak antara puncak yang berbeda. Jadi, jika seseorang memilih dua titik pada lanskap yang luas ini – yaitu, dua “solusi” yang mungkin – keduanya akan sangat dekat (jika berasal dari puncak yang sama) atau sangat berjauhan (jika diambil dari puncak yang berbeda) . Dengan kata lain, akan ada tanda “celah” dalam jarak ini – kecil atau besar, tetapi tidak ada di antaranya. Kredit: David Jamarnik dkk.
Gagasan bahwa beberapa masalah komputasi dalam matematika dan ilmu komputer dapat menjadi sulit seharusnya tidak mengejutkan. Faktanya, ada seluruh kelas masalah yang dianggap mustahil untuk diselesaikan secara matematis. Di bawah kategori ini ada beberapa masalah “lebih mudah” yang tidak dipahami dengan baik – dan mungkin juga tidak mungkin.
David Jamarnik, Profesor Riset Operasi di MIT Sloan School of Management dan Institut Data, Sistem, dan Masyarakat, memusatkan perhatiannya pada kategori terakhir dari masalah yang kurang dipelajari, yang lebih relevan dengan dunia sehari-hari karena melibatkan Acak—Sebuah fitur integral dari sistem alam. Dia dan rekan-rekannya telah mengembangkan alat yang ampuh untuk menganalisis masalah ini yang disebut properti celah yang tumpang tindih (atau OGP). Gamarnik menggambarkan metodologi baru dalam makalah penelitian baru-baru ini di Prosiding National Academy of Sciences.
P NP
Lima puluh tahun yang lalu, masalah paling terkenal dalam ilmu komputer teoretis dirumuskan. P NP bertanya, apakah ada masalah yang melibatkan kumpulan data besar yang jawabannya dapat diverifikasi dengan relatif cepat, tetapi – bahkan jika bekerja pada komputer tercepat yang tersedia – akan membutuhkan waktu yang sangat lama untuk diselesaikan.
Dugaan P NP tetap tidak terbukti, namun sebagian besar ilmuwan komputer percaya bahwa banyak masalah yang sudah dikenal—termasuk, misalnya, masalah penjual keliling—termasuk dalam kategori yang sangat sulit ini. Tantangan dalam contoh penjual adalah menemukan rute terpendek, dalam hal jarak atau waktu, melalui N kota yang berbeda. Tugas mudah dikelola ketika N = 4, karena hanya ada enam jalur yang mungkin untuk dipertimbangkan. Tapi di 30 kota, ada lebih dari 1030 cara yang mungkin, dan jumlahnya naik secara eksponensial dari sana. Kesulitan terbesar terletak pada mendesain file algoritma Ini memecahkan masalah dengan cepat dalam semua kasus, untuk semua nilai bilangan bulat N., ilmuwan komputer yakin, berdasarkan teori kompleksitas komputasi, bahwa tidak ada algoritma seperti itu, membenarkan bahwa P NP.
Ada banyak contoh lain dari masalah yang sulit dipecahkan seperti itu. Misalkan, misalnya, Anda memiliki tabel angka besar dengan ribuan baris dan ribuan kolom. Dapatkah Anda menemukan, dari semua kombinasi yang mungkin, susunan yang tepat dari sepuluh baris dan 10 kolom sedemikian rupa sehingga seratus entri mereka memiliki jumlah tertinggi yang dapat dicapai? “Kami menyebutnya tugas pengoptimalan, karena Anda selalu berusaha menemukan yang terbesar atau terbaik — jumlah angka terbesar, rute terbaik melalui kota, dll.,” kata Jamarnik.
Ilmuwan komputer telah lama menyadari bahwa Anda tidak dapat membuat algoritme cepat yang, dalam semua kasus, dapat memecahkan masalah seefisien kisah penjual keliling. “Kemungkinan hal seperti itu tidak mungkin untuk alasan yang dipahami dengan baik,” catat Jamarnik. “Tetapi dalam kehidupan nyata, alam tidak menghasilkan masalah dari sudut pandang yang tidak bersahabat. Ia tidak mencoba membuat Anda frustrasi dengan masalah yang dipilih dengan cermat dan paling menantang.” Faktanya, orang biasanya menghadapi masalah dalam keadaan yang lebih acak dan kurang terkelola, dan inilah masalah yang ingin ditangani oleh Kemitraan Pemerintah Terbuka.
Puncak dan lembah
Untuk memahami apa itu Kemitraan Pemerintah Terbuka, mungkin ada baiknya untuk melihat dulu bagaimana gagasan itu muncul. Sejak tahun 1970-an, fisikawan telah mempelajari kaca spin – bahan yang memiliki sifat cair dan padat yang memiliki perilaku magnetik yang tidak biasa. Penelitian tentang kacamata spin telah memunculkan teori umum tentang sistem kompleks yang terkait dengan masalah dalam fisika, matematika, ilmu komputer, ilmu material, dan bidang lainnya. (Karya ini memenangkan Giorgio Baresi Hadiah Nobel Fisika 2021.)
Satu masalah membingungkan yang dihadapi fisikawan adalah mencoba memprediksi keadaan energi, khususnya konfigurasi energi terendah, dari struktur kaca pemintalan yang berbeda. Situasi ini kadang-kadang digambarkan dalam “pemandangan” puncak gunung yang tak terhitung jumlahnya yang dipisahkan oleh lembah, di mana tujuannya adalah untuk menemukan puncak tertinggi. Dalam hal ini, puncak tertinggi sebenarnya mewakili keadaan energi terendah (walaupun seseorang dapat membalik gambar dan mencari lubang terdalam). Ini ternyata menjadi masalah pengoptimalan yang mirip dengan dilema penjual keliling, Jamarnik menjelaskan: “Anda memiliki rangkaian gunung yang sangat besar, dan sepertinya satu-satunya cara untuk menemukan yang lebih tinggi adalah dengan mendaki masing-masing gunung”—tugas yang tidak masuk akal serupa untuk menemukan jarum di tumpukan jerami.
Fisikawan telah menunjukkan bahwa Anda dapat menyederhanakan gambar ini, dan mengambil langkah menuju solusi, dengan memotong gunung ke ketinggian tertentu yang telah ditentukan dan mengabaikan segala sesuatu di bawah tingkat batas tersebut. Anda kemudian akan meninggalkan sekelompok puncak yang menonjol di atas lapisan awan yang seragam, dengan setiap titik di puncak tersebut mewakili solusi potensial untuk masalah awal.
Dalam makalah penelitian 2014, Jamarnik dan rekan mencatat sesuatu yang sebelumnya diabaikan. Mereka menyadari dalam beberapa kasus bahwa diameter setiap puncak akan jauh lebih kecil daripada jarak antara puncak yang berbeda. Jadi, jika seseorang memilih dua titik pada lanskap yang luas ini – yaitu, dua “solusi” yang mungkin – keduanya akan sangat dekat (jika berasal dari puncak yang sama) atau sangat berjauhan (jika diambil dari puncak yang berbeda) . Dengan kata lain, akan ada tanda “celah” dalam jarak ini – kecil atau besar, tetapi tidak ada di antaranya. Jamarnik dan rekan menyarankan agar sistem dalam hal ini bercirikan OGP.
“Kami menemukan bahwa semua masalah yang diketahui dari sifat acak yang sulit secara komputasi memiliki versi properti ini” – yaitu, diameter gunung dalam model skematis jauh lebih kecil daripada jarak antar pegunungan, Jamarnik menegaskan. “Ini memberikan ukuran yang lebih akurat dari kekokohan algoritme.”
Membuka rahasia kompleksitas algoritma
Munculnya OGP dapat membantu peneliti menilai kesulitan membuat algoritma cepat untuk mengatasi masalah tertentu. Ini telah memungkinkan mereka untuk “secara matematis” [and] Dia dengan tegas mengesampingkan kelas besar algoritme sebagai pesaing potensial,” kata Jamarnik. Kami telah mempelajari, khususnya, bahwa algoritme stabil – yang keluarannya tidak akan banyak berubah jika masukannya hanya sedikit berubah – akan gagal menyelesaikan masalah pengoptimalan semacam ini. “Hasil negatif ini tidak hanya berlaku untuk komputer klasik tetapi juga untuk komputer kuantum, dan secara khusus, untuk apa yang disebut “algoritma optimasi pendekatan kuantum” (QAOAs), yang diharapkan beberapa peneliti akan memecahkan masalah optimasi yang sama. Sekarang mengingat hasil Jamarnik dan temuan rekan penulis, harapan ini dilunakkan oleh pengakuan bahwa banyak lapisan operasi akan diperlukan agar algoritme tipe QAOA berhasil, yang secara teknis dapat menantang.
“Apakah ini berita baik atau buruk tergantung pada sudut pandang Anda,” katanya. “Saya pikir itu kabar baik dalam arti membantu kita membuka rahasia kompleksitas algoritmik dan meningkatkan pengetahuan kita tentang apa yang ada di bidang probabilitas dan apa yang tidak. Ini berita buruk dalam arti bahwa ini memberi tahu kita bahwa masalah ini sulit, bahkan jika alam memproduksinya, dan bahkan jika mereka dihasilkan secara acak”. Dia menambahkan bahwa berita tersebut tidak terlalu mengejutkan. “Banyak dari kita telah mengharapkan ini selama ini, tetapi kita sekarang memiliki dasar yang jauh lebih kuat untuk membuat klaim itu.”
Ini masih menyisakan beberapa tahun cahaya bagi para peneliti untuk dapat membuktikan bahwa tidak ada algoritme cepat yang dapat menyelesaikan masalah pengoptimalan ini dalam pengaturan acak. Memiliki bukti tersebut akan memberikan jawaban yang pasti untuk masalah P NP. Dia berkata, “Jika kita dapat membuktikan bahwa kita tidak dapat memiliki algoritme yang bekerja hampir sepanjang waktu, itu memberi tahu kita bahwa kita pasti tidak dapat memiliki algoritme yang berfungsi sepanjang waktu.”
Memprediksi berapa lama waktu yang dibutuhkan sebelum masalah P NP terpecahkan tampaknya menjadi masalah yang sulit dipecahkan. Kemungkinan akan ada banyak puncak untuk didaki, dan lembah untuk dilintasi, sebelum peneliti mendapatkan perspektif yang lebih jelas tentang situasi tersebut.
David Jamarnik, Properti Gap Bersarang: Penghalang Topologis untuk Optimasi Atas Struktur Stokastik, Prosiding National Academy of Sciences (2021). DOI: 10.1073/pnas.2108492118
pengenalan
Institut Teknologi Massachusetts
kutipan: peneliti mengembangkan alat baru untuk memahami masalah komputasi yang sulit dan tampaknya sulit dipecahkan (2022, 10 Januari) Diperoleh pada 11 Januari 2022 dari https://phys.org/news/2022-01-tool-hard-problems-intractable.html
Dokumen ini tunduk pada hak cipta. Sekalipun ada kesepakatan yang adil untuk tujuan studi atau penelitian pribadi, tidak ada bagian yang boleh direproduksi tanpa izin tertulis. Konten disediakan untuk tujuan informasi saja.

“Kutu buku musik lepas. Pecandu internet bersertifikat. Pencinta perjalanan. Penyelenggara hardcore. “










More Stories
Makanan cepat saji dan daging olahan mungkin menjadi penyebab kanker di kalangan anak muda: dokter
Kapan peluncurannya? Bisakah saya melihatnya di New Smirna?
Sebuah studi baru memetakan awal mula kehidupan hewan